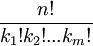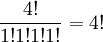Permutasi

Permutasi adalah penyusunan kembali suatu kumpulan objek dalam urutan yang berbeda dari urutan yang semula. Sebagai contoh, kata-kata dalam kalimat sebelumnya dapat disusun kembali sebagai “adalah Permutasi suatu urutan yang berbeda urutan yang kumpulan semula objek penyusunan kembali dalam dari.” Proses mengembalikan objek-objek tersebut pada urutan yang baku (sesuai ketentuan) disebut sorting.

Pengertian[sunting | sunting sumber]

Jika terdapat suatu untai abjad abcd, maka untai itu dapat dituliskan kembali dengan urutan yang berbeda: acbd, dacb, dan seterusnya. Selengkapnya ada 24 cara menuliskan keempat huruf tersebut dalam urutan yang berbeda satu sama lain.

 abcd  abdc  acbd  acdb  adbc  adcb
 bacd  badc  bcad  bcda  bdac  bdca
 cabd  cadb  cbad  cbda  cdab  cdba
 dabc  dacb  dbac  dbca  dcab  dcba

Setiap untai baru yang tertulis mengandung unsur-unsur yang sama dengan untai semula abcd, hanya saja ditulis dengan urutan yang berbeda. Maka setiap untai baru yang memiliki urutan berbeda dari untai semula ini disebut dengan permutasi dari abcd.

Menghitung Banyaknya Permutasi yang Mungkin[sunting | sunting sumber]

Untuk membuat permutasi dari abcd, dapat diandaikan bahwa terdapat empat kartu bertuliskan masing-masing huruf, yang hendak kita susun kembali. Juga terdapat 4 kotak kosong yang hendak kita isi dengan masing-masing kartu:

 Kartu            Kotak kosong
 -----------      ---------------
 a  b  c  d       [ ] [ ] [ ] [ ]

Maka kita dapat mengisi setiap kotak dengan kartu. Tentunya setiap kartu yang telah dipakai tidak dapat dipakai di dua tempat sekaligus. Prosesnya digambarkan sebagai berikut:

Di kotak pertama, kita memiliki 4 pilihan kartu untuk dimasukkan.

 Kartu            Kotak
 -----------      ---------------
 a  b  c  d       [ ] [ ] [ ] [ ]
                   ^ 4 pilihan: a, b, c, d

Sekarang, kondisi kartunya tinggal 3, maka kita tinggal memiliki 3 pilihan kartu untuk dimasukkan di kotak kedua.

 Kartu            Kotak
 -----------      ---------------
 a  *  c  d       [b] [ ] [ ] [ ]
                       ^ 3 pilihan: a, c, d

Karena dua kartu telah dipakai, maka untuk kotak ketiga, kita tinggal memiliki dua pilihan.

 Kartu            Kotak
 -----------      ---------------
 a  *  c  *       [b] [d] [ ] [ ]
                           ^ 2 pilihan: a, c

Kotak terakhir, kita hanya memiliki sebuah pilihan.

 Kartu            Kotak
 -----------      ---------------
 a  *  *  *       [b] [d] [c] [ ]
                               ^ 1 pilihan: a

Kondisi terakhir semua kotak sudah terisi.

 Kartu            Kotak
 -----------      ---------------
 *  *  *  *       [b] [d] [c] [a]

Di setiap langkah, kita memiliki sejumlah pilihan yang semakin berkurang. Maka banyaknya semua kemungkinan permutasi adalah 4×3×2×1 = 24 buah. Jika banyaknya kartu 5, dengan cara yang sama dapat diperoleh ada 5×4×3×2×1 = 120 kemungkinan. Maka jika digeneralisasikan, banyaknya permutasi dari n unsur adalah sebanyak 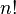$n!$ .

Bilangan Inversi[sunting | sunting sumber]

Setiap permutasi dapat kita kaitkan dengan barisan bilangan yang disebut sebagai barisan bilangan inversi. Setiap unsur dalam permutasi dikaitkan dengan sebuah bilangan yang menunjukkan banyaknya unsur setelah unsur tersebut, yang posisinya salah. Sebagai contoh, salah satu permutasi dari untai abcdefg adalah dacfgeb. Maka untuk setiap unsur dacfgeb dapat dibuat bilangan inversinya:

Posisi	Unsur	Bilangan
0	d	3	Ada 3 huruf setelah posisi 0, yang seharusnya berada sebelum d, yaitu a, b, dan c.
1	a	0	Tidak ada huruf setelah posisi 1, yang seharusnya berada sebelum a.
2	c	1	Ada 1 huruf setelah posisi 2, yang seharusnya berada sebelum c, yaitu b.
3	f	2	Ada 2 huruf setelah posisi 3, yang seharusnya berada sebelum f, yaitu e, dan d.
4	g	2	Ada 2 huruf setelah posisi 4, yang seharusnya berada sebelum g, yaitu e, dan b.
5	e	1	Ada 1 huruf setelah posisi 5, yang seharusnya berada sebelum g, yaitu b.
6	b	0	Tidak ada huruf setelah b.

Maka barisan bilangan inversi dari dacfgeb adalah 3, 0, 1, 2, 2, 1, 0.

Faktoradik[sunting | sunting sumber]

Barisan bilangan inversi dapat dimengerti sebagai sebuah sistem bilangan, yang setiap digitnya memiliki sifat:

a_i \in N

dan

0 \leq a_i \leq i

Sistem bilangan ini disebut sebagai faktoradik. Masing-masing faktoradik dapat diubah maupun dibentuk dari bilangan desimal. Ini berguna untuk dapat menghasilkan permutasi ke-k dari sebuah untai.

Membangkitkan Permutasi[sunting | sunting sumber]

Permasalahan umum yang terdapat seputar membangkitkan permutasi adalah:

Diberikan sebuah untai S, tentukan:

Semua permutasi dari S
Semua permutasi n-elemen dari S
Permutasi berikutnya setelah S
Permutasi ke-k dari s sesuai urutan leksikografik (atau aturan lainnya)

Jenis-jenis Permutasi Lainnya[sunting | sunting sumber]

Permutasi-k dari n benda[sunting | sunting sumber]

Terkadang kita hanya ingin menyusun ulang sejumlah elemen saja, tidak semuanya. Permutasi ini disebut permutasi-k dari n benda. Pada contoh untai abcd, maka permutasi-2 dari abcd (yang semuanya ada 4 unsur) adalah sebanyak 12:

 ab  ac  ad
 ba  bc  bd
 ca  cb  cd
 da  db  dc

Sedangkan permutasi-3 dari untai yang sama adalah sebanyak 24:

 abc  abd  acb  acd  adb  adc
 bac  bca  bad  bda  bcd  bdc
 cab  cba  cad  cda  cbd  cdb
 dab  dba  dac  dca  dbc  dcb

Banyaknya kemungkinan permutasi seperti ini adalah

P^n_k = \frac{n!}{(n-k)!}

Permutasi dengan elemen yang identik[sunting | sunting sumber]

Terkadang tidak semua unsur dalam permutasi dapat dibedakan. Unsur-unsur ini adalah unsur-unsur yang identik atau sama secara kualitas. Suatu untai aabc terdiri dari 4 macam unsur, yaitu a, b, dan c tetapi unsur a muncul sebanyak dua kali. Kedua a tersebut identik. Permutasi dari aabc adalah berjumlah 12:

 aabc  aacb  abac  abca
 acab  acba  baac  baca
 bcaa  caab  caba  cbaa

Ini bisa dimengerti sebagai permutasi biasa dengan kedua unsur a dibedakan, yaitu a₀ dan a₁:

   a₀a₁bc  a₁a₀bc  =  aabc
   a₀a₁cb  a₁a₀cb  =  aacb
   a₀ba₁c  a₁ba₀c  =  abac
   a₀bca₁  a₁bca₀  =  abca
   a₀ca₁b  a₁ca₀b  =  acab
   a₀cba₁  a₁cba₀  =  acba
   ba₀a₁c  ba₁a₀c  =  baac
   ba₀ca₁  ba₁ca₀  =  baca
   bca₀a₁  bca₁a₀  =  bcaa
   ca₀a₁b  ca₁a₀b  =  caab
   ca₀ba₁  ca₁ba₀  =  caba
   cba₀a₁  cba₁a₀  =  cbaa

Total permutasi dari untai aabc adalah sebanyak 4! = 24. Tetapi total permutasi ini juga mencakup posisi a₀ dan a₁ yang bertukar-tukar, yang jumlahnya adalah 2! (karena a terdiri dari 2 unsur: a₀ dan a₁). Dengan demikian jika dianggap a₀ = a₁ maka banyak permutasinya menjadi 4! dibagi dengan 2!. Cara menghitung ini dapat digeneralisasikan:

Untuk untai S sepanjang n yang mengandung satu macam unsur identik sebanyak k:

\frac{n!}{k!}

Lebih umum lagi, jika panjang untai adalah n, mengandung m macam unsur yang masing-masing adalah sebanyak k₁, k₂, …, k_m, maka:

\frac{n!}{k_1! k_2! ... k_m!}

atau

\frac{n!}{\prod_{i=1}^m{k_i!}}

Sebagai contoh, untai aaaaabbcccdddddd terdiri dari 5 a, 2 b, 3 c, dan 6 d, maka banyaknya permutasi yang dapat dibentuk:

\frac{16!}{5! 2! 3! 6!} = 20180160

Dalam permutasi biasa, misalnya abcd, setiap unsur hanya muncul satu kali, sehingga

\frac{4!}{1! 1! 1! 1!} = 4!

Unsur yang identik tersebut tidak perlu benar-benar identik, tetapi bisa merupakan unsur yang berbeda, tetapi ada kualitas tertentu yang kita anggap sama dari kedua unsur tersebut. Sebagai contoh, huruf A dan huruf a bisa dianggap identik untuk keperluan tertentu.

Permutasi siklis[sunting | sunting sumber]

Permutasi siklis menganggap elemen disusun secara melingkar.

Pada susunan di atas, kita dapat membaca untai tersebut sebagai salah satu dari untai-untai berikut:

 abcdefgh
 bcdefgha
 cdefghab
 defghabc
 efghabcd
 fghabcde
 ghabcdef
 habcdefg

Cara membaca untai abcdefgh dalam susunan melingkar tersebut bermacam-macam, maka setiap macam cara kita anggap identik satu sama lain. Permutasi siklis dapat dihitung dengan menganggap bahwa satu elemen harus ditulis sebagai awal untai.

 a bcdefgh
   --------
   ^ bagian yang dipermutasikan

Dengan menganggap panjang untai (atau banyaknya elemen) adalah n, dan karena elemen awal tidak boleh diubah-ubah posisinya, maka banyaknya elemen yang dapat berubah-ubah posisinya adalah n-1. Dengan demikian kita cukup mempermutasikan elemen yang dapat berubah-ubah posisi saja, yaitu sebanyak 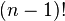$(n-1)!$ .

Lihat pula[sunting | sunting sumber]

Pranala luar[sunting | sunting sumber]

sumber:https://id.wikipedia.org/wiki/Permutasi