A.PENGERTIAN MATRIKS
Matriks adalah kumpulan bilangan , simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Penemu matriks adalah Arthur Cayley.
Syarat – syarat suatu matriks :
○ Unsur – unsurnya terdiri dari bilangan – bilangan
○ Mempunyai baris dan kolom
○ Elemen – elemennya berbentuk persegi panjang dalam kurung biasa , kurung siku , atau kurung bergaris dua.
Fungsi matriks dalam kehidupan sehari-hari :
● Matriks banyak dimanfaatkan untuk menyelesaikan berbagai permasalahan matematika misalnya dalam menemukan solusi masalah persamaan linear, transformasi linear yakni bentuk umum dari fungsi linear contohnya rotasi dalam 3 dimensi. Matriks juga seperti variabel biasa, sehingga matrikspun dapat dimanipulasi misalnya dikalikan, dijumlah, dikurangkan, serta didekomposisikan. Menggunakan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur.
● Memudahkan dalam membuat analisis mengenai suatu masalah ekonomi yang mengandung bermacam – macam variable.
● Digunakan dalam memecahkan masalah operasi penyelidikan , misalnya masalah operasi penyelidikan sumber – sumber minyak bumi dan sebagainya.
● Dikaitkan dengan penggunaan program linear, analisis input output baik dalam ekonomi, statistic, maupun dalam bidang pendidikan, manajemen, kimia, dan bidang – bidang teknologi yang lainnya.
● Dengan menggunaan Microsoft Office Excel sebagai media pembelajaran. Khususnya untuk menghitung berbagai operasi matriks ternyata cukup mudah untuk dilakukan oleh guru serta sangat efisien untuk waktu pengerjaan sebuah matriks, jika secara manual untuk menghitung sebuah matriks yang memiliki orde banyak diperlukan waktu yang sangat lama bahkan sampai berhari-hari. Tetapi dengan menggunakan fungsi matriks untuk menghitungnya dapat dilakukan hanya dengan beberapa menit saja. Apalagi dengan menggunakan Microsoft Office Excel sebagai media pembelajaran, cukup mudah dilaksanakan dan sangat efektif digunakan sebagai alat bantu untuk membuat soal-soal latihan interaktif. Hanya saja dibutuhkan keahlian dan daya imaginasi guru tersebut untuk mengembangkan media pembelajaran dengan menggunakan Microsoft Office Excel.
B. TRANSPOSE SUATU MATRIKS ( notasinya At atau A, )
Transpose suatu matriks adalah matriks baru yang diperoleh dari suatau matriks asal dengan mempertukarkan antara elemen kolom dan elemen barisannya.
Jika diketahui suatu matriks A dengan ordo m × n, maka transpose matriks tersebut adalah matriks berordo n × m. Transpos A adalah matriks baru dimana elemen kolom pertama = elemen baris pertama matriks A, elemen kolom kedua = elemen baris kedua matriks A, elemen kolom ketiga= elemen baris ketiga matriks A.
Misal Matriks A =
Maka Transpos A adalah At =
Jadi jika ordo matriks A = 3×4 maka ordo matriks transpos adalah 4×3
Sifat-sifat matriks transpose :
1) ( A + B )t = At + Bt
2) ( At )t = A
3) ( AB )t = Bt At
4) ( kA )t = kAt, dengan k = konstanta
Dalam pembahasan transpose dikenal istilah matriks simetri, yaitu matriks yang sama transposenya. Matriks Simetri merupakan suatu matriks bujur sangkar yang unsur pada baris ke-i kolom ke-j sama dengan unsur pada baris ke-j kolom ke-i sehingga .
Contoh : G =
Unsur pada baris ke-2 kolom ke-4 adalah 9 dan unsur pada baris ke-4 kolom ke-2 juga 9.
C. KESAMAAN MATRIKS
Kesamaan antara dua matriks tidak hanya ditentukan oleh kesamaan ordo kedua matriks itu. Dua matriks dikatakan sama ( identik ) jika ordo keduamatriks itu sama dan elemen – elemen yang bersesuaian pada kedua matriks sama nilainya. Matriks A dan matriks B dikatakan berordo sama atau berukuran sama jika banyaknya baris dan banyaknya kolom pada matriks A sama dengan banyaknya baris dan banyaknya kolom pada matriks B
Contoh :
A = dan B =
Matriks A berordo sama dengan matriks B, yaitu
Definisi:
Dua buah matriks A dan B dikatakan sama, ditulis A = B, jika dan hanya jika :
a. Matriks A dan B mempunyai ordo sama
b. Unsur-unsur yang seletak pada matriks A dan matriks B sama.
D. OPERASI ALJABAR PADA MATRIKS
Pada operasi aljabar dapat berupa penjumlahan atau pengurangan matriks dan perkalian matriks.
1. Penjumlahan pada Matriks
Dua matriks dapat dijumlahkan atau dikurangkan jika ordonya sama. Misal ordo matriks A = 2 x 3 dan ordo matriks B = 2 x 3, maka keduanya dapatdijumlahkan atau dikurangkan.
Contoh : Jika A = dan B =
Maka A + B = =
A – B = =
Adapun beberapa sifat dasar yang dimiliki operasi penjumlahan pada matriks. Untuk A, B, C, dan 0 ( matriks nol ) yang merupakan matriks – matriks berordo yang sama, berlaku sifat – sifat berikut :
1) A + B = B + A ( sifat komutatif )
2) A + (B + C ) = ( A + B ) + C ( sifat asosiatif )
3) Terdapat matriks identitas penjumlahan, yaitu matrik nol sehingga berlaku A + 0 = 0 + A = A untuk setiap matriks A.
4) Terdapat invers penjumlahan sehingga berlaku A + (- A) = – A + A = 0, yang dimaksud dengan matriks – A atau matriks lawan dari matriks A adalah matriks yang elemen – elemennya merupakan negative dari elemen – elemen dari matriks A yang seletak.
2. Pengurang pada Matriks
Pada prinsipnya, operasi pengurangan pada matrik sama dengan operasi penjumlahan pada matrik. Sehingga sifat – sifat pada operasi pengurangan pada matrik sama dengan operasi pengurangan pada metriks, yaitu :
1) A – B = A + (- B )
2) A – B = C
3) A + B = C, maka berarti B = C – A dan A = C – B
3. Perkalian pada Matriks
Operasi perkalian pada matriks terdiri dari operasi perkalian antara matriks dengan suatu scalar dan perkalian antarmatriks (matriks dengan matriks).
3.1 Perkalian antara Matriks dengan Skalar
Jika A suatu ordo m n dan k suatu bilangan real (disebut juga sutu skalar), maka kA adalah metriks ordo m n yang unsur-unsurnya diperoleh dengan memperkalikan setiap unsur matriks A dengan k. Perkalian seperti ini disebut perkalian skalar.
Jadi, jika A , maka: kA
Contoh : Misal A = maka 3A = 3 =
Sifat-sifat perkalian matriks dengan bilangan real.
Jika a dan b bilangan real, maka :
1) ( a + b )A = aA + bA
2) a ( A + B ) = aA + aB
3) a( bA ) = (ab)A
4) 1 × A = A
5) 0 × A = 0
6) (- 1) A = – A
3.2 Perkalian antar Matriks
Matriks A yang berordo m p dangan suatu matriks B yang berordo p n adalah matriks C
yang berordo m n.
A m p.B p n = C m n.
Dalam perkalian matriks ini yang perlu diperhatikan adalah :
Banyaknya kolom pada matriks A harus sama dengan banyaknya baris pada matriks B.
Jika hal ini tidak dipenuhi, maka hasil kali matriks tidak didefinisikan.
Secara umum jika A = ordo matriks 2 3
B = ordo matriks 3 2
C = A . B
= ordo matriks 2 2
E. INVERS DAN DETERMINAN
1. Menentukan Determinan dan Invers
1). Determinan Matriks Persegi Berordo 2
Matriks A =
Hasil kali elemen-elemen diagonal utama dikurangi hasil kali elemen-elemen diagonal
samping disebut determinan matriks A.
Notasi determinan matriks A adalah atau det A = ad – bc
Contoh : Jika A = maka det A =
= ( 1)(4) – (2)(-3)
= 4 +6
= 10
2). Determinan Matriks Persegi Berordo 3
Matriks A =
Cara menentukan det A sebagai berikut :
Cara 1 : det A =
=
Cara 2 : menggunakan aturan Saurrus
det A =
– – – + + +
=
3). Invers Matriks Bujur Sangkar
Jika A dan B matriks ordo n x n, maka B adalah invers matriks A atau B adalah invers dari matriks A dan hanya jika AB = BA = I, I adalah matriks identitas.
Contoh : Misal A = dan B =
Maka BA = = = I
Dengan demikian, B adalah invers dari A, di tulis B = A-1.Oleh karena BA = I dan B = A-1
maka A-1A = I
Jika A = maka invers A (ditulis A-1)
dan dirumuskan
Harga (ad –bc) disebut determinan dari matriks A atau det A.
Matriks mempunyai invers jika dan hanya jika (ad – bc) 0.
Jika (ad – bc) = 0 maka matriks tidak mempunyai invers.Matriks yang
determinannya = 0, dinamakan matriks Singular.
Sifat sifat invers matriks dan penggunaanya
a. Sifat sifat invers matriks
Diketahui matrik A dan B adalah matriks persegi, A-1 invers dari A dan B-1 invers dari B, serta I matriks identitas, maka berlaku sifat sifat invers matriks sebagai berikut:
1. AA-1 = A-1A = I
2. (A-1)-1 = A
3. (AB)-1 = B-1A-1
4. (At)-1 = (A-1)t
Sifat sifat invers matriks matriks hanya berlaku pada matriks non singular
Penyelesaian Persamaan Linier Dengan Matriks
1). Penyelesaian Persamaan Linier dua variabel dengan cara determinan
Untuk menyelesaikan persamaan linier dua variabel yang bentuknya seperti berikut
Diubah dalam susunan bilangan sebagai berikut dan diberi notasi D , Dx dan Dy dengan
D = =
Dx = =
Dy = =
F. MACAM-MACAM MATRIKS :
a. Matriks Nol
Matriks nol adalah matriks yang semua elemennya bernilai nol.
b. Matriks Baris
Matriks baris adalah matriks yang hanya terdiri atas satu baris saja.
c. Matriks Kolom
Matriks kolom adalah matriks yang terdiri atas satu kolom.
d. Matriks Persegi
Matriks persegi adalah matriks yang banyak baris dan banyak kolomnya sama.
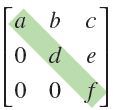
e. Matriks Segitiga Atas
Matriks segitiga atas adalah matriks persegi yang elemen di bawah diagonal utamanya bernilai nol.
f. Matriks Segitiga Bawah
Matriks segitiga bawah adalah matriks persegi yang elemen di atas diagonal utamanya bernilai nol.
g. Matriks Diagonal
Matriks diagonal adalah matriks persegi yang elemen – elemennya bernilai nol, kecuali pada diagonal utamanya tidak selalu nol.
h. Matriks Identitas
Matriks identitas adalah matriks skalar yang elemen – elemen pada diagonal utamanya bernilai 1.
- Contoh MATRIKS NOL
- Contoh MATRIKS BARIS
- Contoh MATRIKS KOLOM
- Contoh MATRIKS PERSEGI
- Contoh SEGITIGA ATAS
- Contoh MATRIKS SEGITIGA BAWAH
- Contoh MATRIKS DIAGONAL
- Contoh MATRIKS IDENTITAS



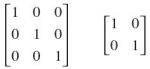
Recent Comments